VIVACE (Vortex Induced Vibration Aquatic Clean Energy)
With the increasing effects of global warming and greenhouse gases, alternative renewable energy sources have been a point of focus for many academic and industrial efforts. In the aquatic environment quite a few clean energy convertors have been proposed to extract the energy of both water currents (like Marine Turbines) and surface waves (like: Pelamis or Oscillating Water Columns) but none of them is capable of efficient energy extraction from slow thermal currents (below 1.5 m/s) of oceans that account for more that 90 percent of the total available energy.
In 2008, Dr. Bernitsas’s team from University of Michigan presented the VIVACE energy convertor which can be used to efficiently extract energy from these slow currents and thus making this vast energy source accessible.
What we have done
In my master degree thesis I worked extensively on building a laboratory model capable of efficient production of electricity in the range of 1.2×105 < Re < 2.2×105. For the first time a vortex induced vibration energy convertor with very low mass ratio (m= 0.36) in high Reynolds current was investigated. A VIV amplitude ratio of 2.49 was established at Reynolds number of 210000 and the maximum extracted power reached 18 watts. It was shown that without damping coefficient, the amplitude of vibrations will constantly increase with increase in flow velocity and a new record for pure VIV vibration was recorded at 2.49. This high amplitude ratio has not been reported from any other experiments. In addition when the mass ratio is under the critical value of 0.45 the lock-in region is expected to be expanded to the infinity, as a result our energy convertor is able to continue its efficient operation in a broad working conditions.
How it works
In the vortex induced vibration energy convertor an elastically mounted cylinder is allowed to vibrate in the vertical direction. When water current passes the smooth circular cylinder, vortex formation and alternating vortex shedding from the top and bottom boundary layers creates an oscillating pressure distribution around the cylinder. Thereby creating an oscillating lift force causing the body to experience vortex-induced vibration. When the frequency of this vibrations is near the natural frequency of the system lock-in phenomenon occurs and the cylinder will resonate. Then this amplified energy in motion of the cylinder is converted to electricity.
Test Apparatus
In my project the objective was to investigate the VIV in very low mass ratio, and to bring down the mass ratio the dimensions of the model had to be large enough that the high cylinder buoyancy would bring the mass ratio under 0.4. The towing tank at the National Iranian Marine Laboratory was 6 meters in width and 400 meters long and 4 meters in depth, which gave us plenty of room to test the larger model. As it can be seen from fig. 1, the experimental model consists of 6 main parts.
- First is the main cylinder that is a 125 millimeters diameter, 1.25 meter length UPVC pipe. This brings the total weight of the moving parts and the mass ratio down significantly, as the weight of the UPVC pipe is very low and the buoyancy force is nearly 15 kilograms.
- Second is the main structure, which is constructed from available steel profiles. It’s 3.5 meters in height and 1.5 meters in width it can be attached to the underside of the towing tank carriage. Then there is two straight shafts and four linear bearings which constrain the cylinder’s motion to move only in the vertical axes.
- A system of pulley and wire rope was utilized to transfer the vertical oscillating motion of the cylinder to the main shaft that would then transfer the rotational motion to the encoder and power take of units (in the right and left hand of the picture below respectively).
- A 500 pulse optical encoder connected to an Arduino Due board was used to calculate the vertical position of the cylinder with an accuracy of about 0.1 millimeters with high data acquiring speed.
- The role of the gear unit is to make the alternating rotational motion of the shaft one directional and also increase the shaft rotational speed by a factor of three. This was done (fig. 2) using two sets of sprockets and chains connected together through a simple gear mechanism that would make the two sprockets rotate in opposite directions and a set of clutch bearings were used on the sprockets which would be activated alternatingly in the opposite directions. In this way the motor shaft would always rotate clockwise whether the cylinder goes down or comes up (see the video). This system can significantly increase the generator’s efficiency.
- Then electric power would be harvested by an electrical generator that is a permanent magnet 300 watts, 36 volts and 1100 rpm DC motor wired in generator mode.

Fig 1. Experimental model attached to the underside of carriage

Fig 2. Gearbox and transmission system
For control and measurement of the extracted power, a set of varying resistors (rheostat) were added to the generator circuit and the voltage was measured using the Arduino due board. This way the generated current relative to time could be recorded and the damping coefficient induced by the generator on the oscillating cylinder could be adjusted.
Different physical properties of the system is depicted in table 1.
| Mass Ratio | m* | 0.36 |
| Damping Ratio of Harvested Energy | Rharn [ohm] | 70, 85, 100, 125 |
| Oscillating Mass | M [kg] | 5.5 |
| Diameter of the Circular Cylinder | D [m] | 0.125 |
| Spring Stiffness | K [N/m] | 480 |
| Structural Damping | Cstructure [Ns/m] | 3.4 |
| Natural Frequency in Water | fn,water [Hz] | 0.765 |
| Dynamic Viscosity of Water | μ [ns/m2] | 8.899E-04 |
| Water Density | ρ [kg/m3] | 997 |
Experimental Results
For the four set of harnessing resistances in table 1, amplitude and extracted power was measured for different flow velocities (1.2×105 < Re < 2.2×105) to establish the VIV characteristics of the model in very low mass ratio of 0.36. The results for VIV without gear and generator attached (Fig. 2), show that with increase in flow velocity the amplitude of oscillations constantly increases and does not decline at higher flow velocities. This is due to the very low mass ratio of the system and confirms the predictions made by Williamson et al.
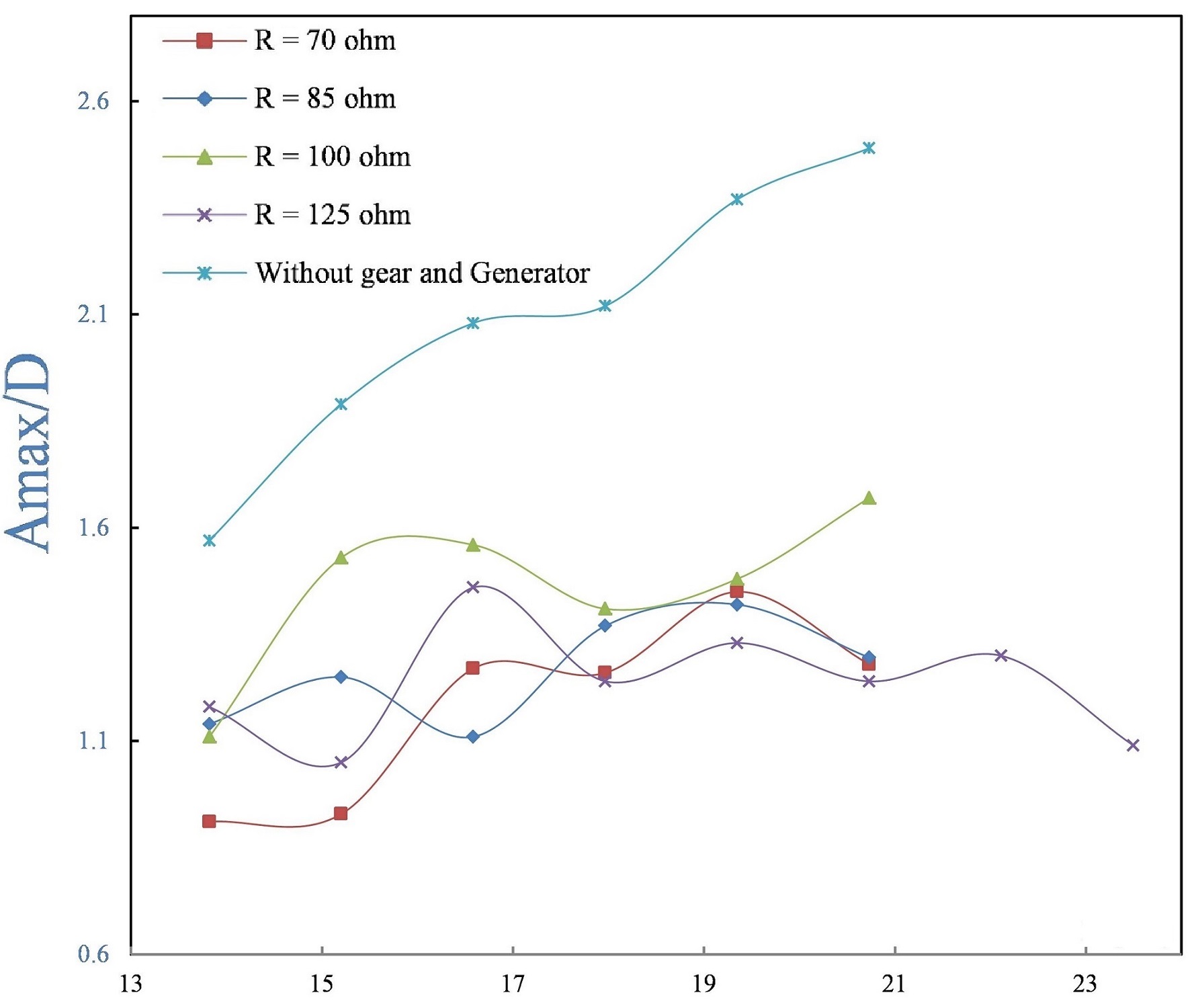
Fig 3. VIV amplitude ratio vs Reynolds number
Figure 4 shows the dominant frequency of oscillating cylinder against increasing flow velocities. It can be seen that the overall frequency of vibrations remains more or less constant in the entire range. And the frequency ratio is well above 1. This is purely due to very low mass ratio of the system and the effects of variable added mass. The Fourier analysis of the vibrations (fig. 5) on the other hand, shows a dominant frequency in the vortex shedding and the resulting oscillations which clearly suggests an established vortex shedding mode.
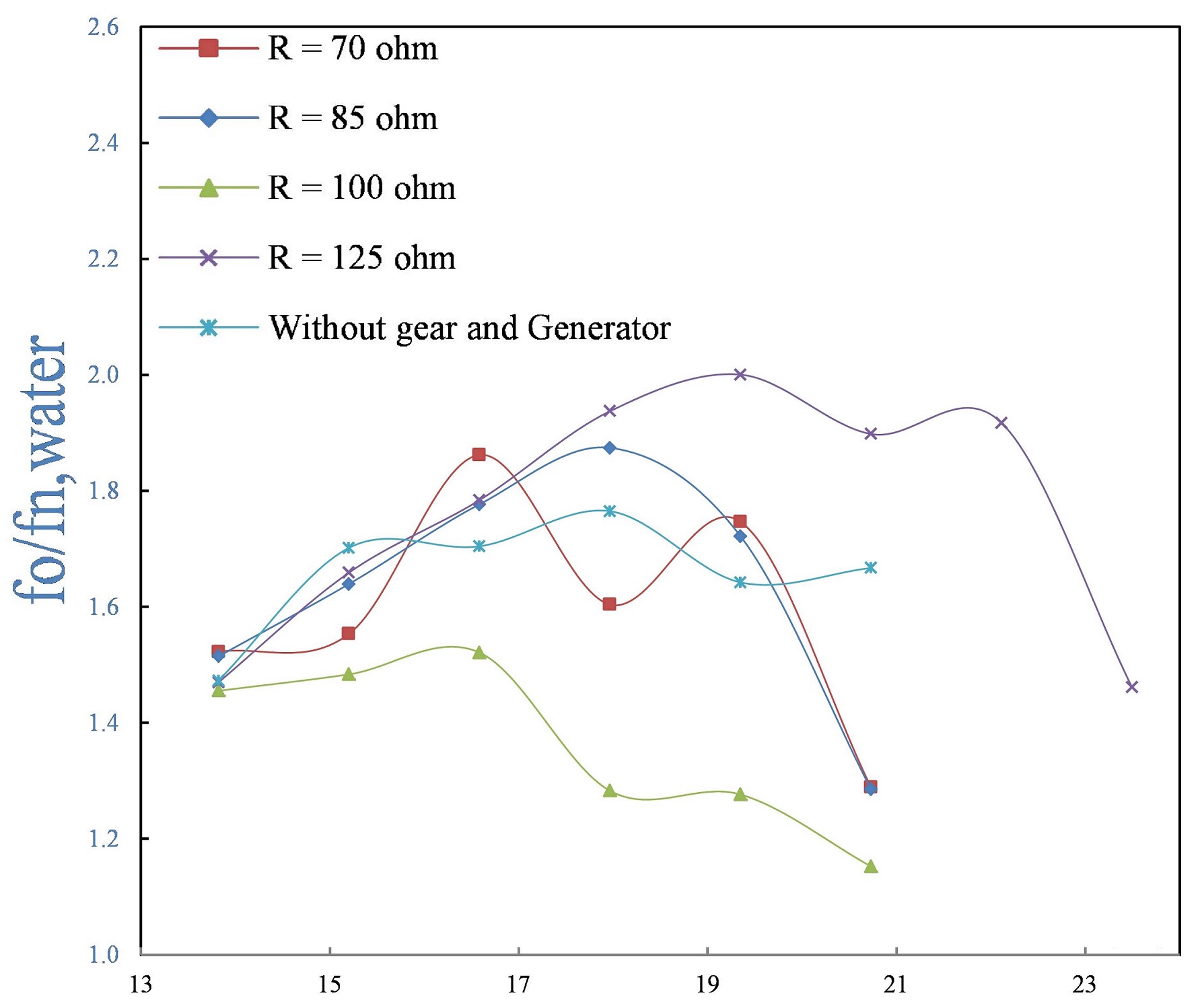
Fig 4. VIV amplitude ratio vs Reynolds number
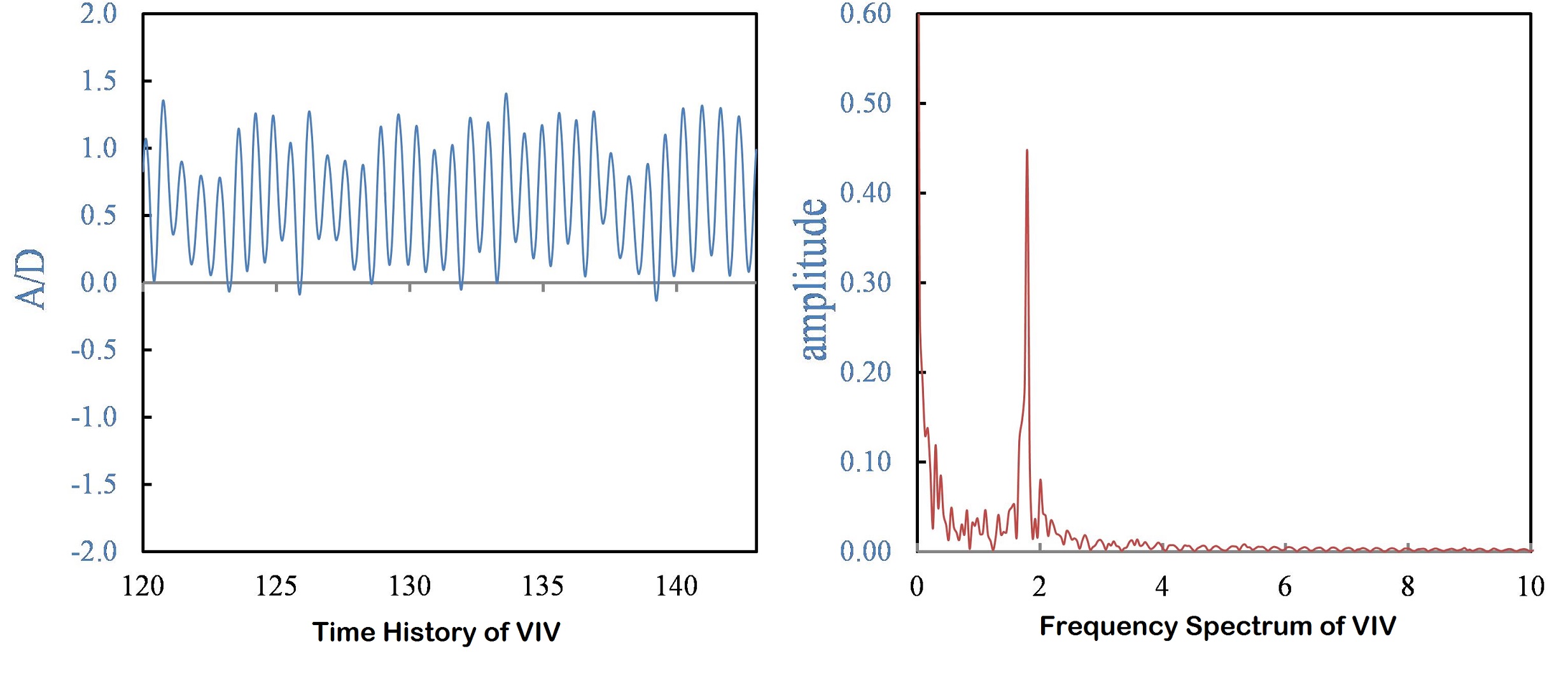
Fig 5. Fourier analysis of VIV amplitude with R=100 ohm at Re=180000
